中学校・高等学校 数学活用法
中学校・高等学校の数学でのロイロノートの活用方法をまとめました。
数と式に関する内容
数の概念と式の計算
正負の数、文字式、整式の加減乗除、平方根、有理数・無理数、因数、複素数、分数式、剰余の定理や因数定理などを扱い、数の性質や不等式を通して論理的な思考をおこなうこの分野では、カードの並べ替えや手書き機能が非常に便利です。また、共有ノートで協働的に学びを進めることで、抽象的でわかりにくい数式の取り扱いや概念も理解がスムーズになります。
手書き・カードの並べ替えで、問題をわかりやすく
ロイロでは写真・カードなどに簡単に手書きで書き込むことができます。そのため、立式にあたってどのように数を分けて考えたかがわかりやすく表現でき、理解がしやすくなります。
さらに、カードを動かしながら状況を整理することで問題に書かれた状況を理解しやすくなります。

参考リンク
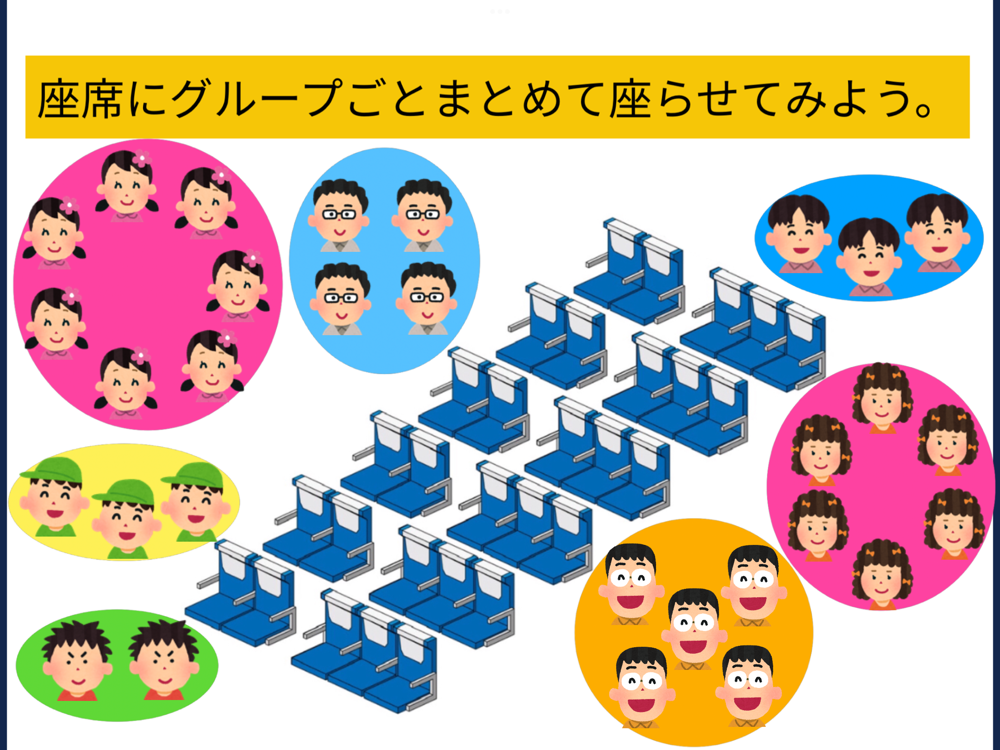
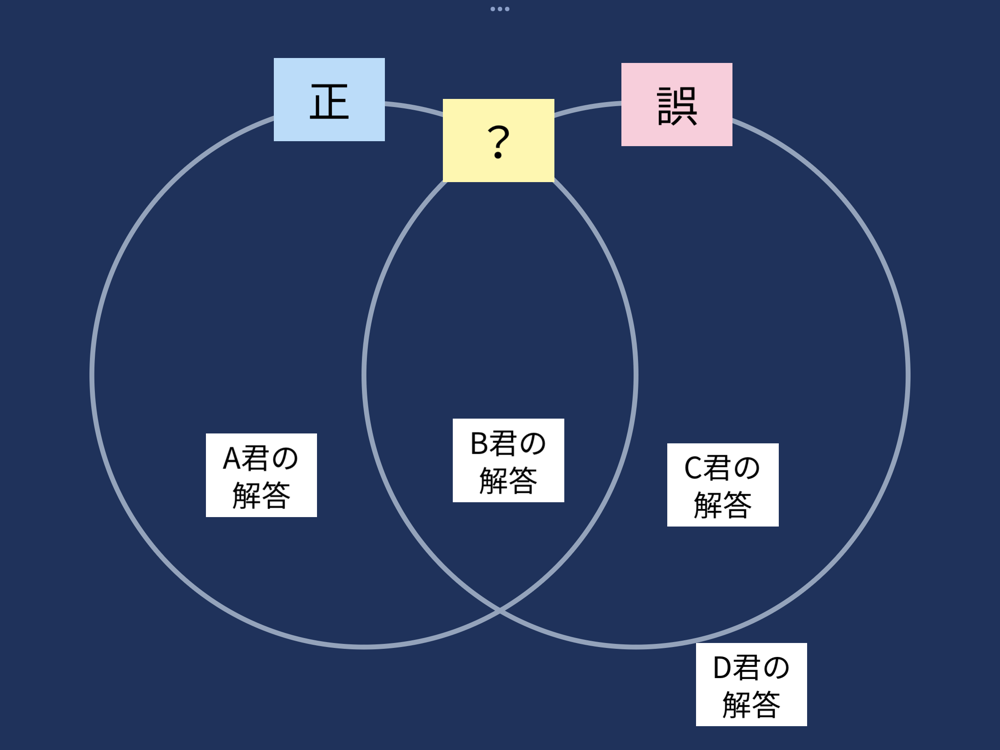
シンキングツールで文字式の特徴や正誤を分類
シンキングツールをつかうことで、文字式を特徴ごとに分類したり、正誤を判別しながら問題を考えることができます。
カードの上に数式を並べて、視点をもって分類していくことで抽象的な文字式の概念が理解しやすくなります。


参考リンク
方程式と不等式
一次方程式、連立方程式、二次方程式、複素数の範囲での解の扱い、高次方程式や複二次方程式の解法を学び、解の性質や関係について理解することを目的とした分野では、テストカードで理解度を確認するアプローチがとても有効です。
さらに最適な解法を選択する必要のある同分野では、提出箱によって、お互いの回答を比較したり、共有ノートでリアルタイムで意見を交換するするアプローチもとても有効です。
テストカードで理解度の確認
反復演習が必要となるこの単元では、テストカードの自動採点機能がとても有効です。
生徒はテストカードで理解度を確認することで、自分のつまづきを自覚し、効率よく問題演習をすすめることができます。



参考リンク
提出箱でお互いの解法を比較
最適な解法を選ぶことも大切なこの分野では、提出箱でお互いの解法を比較することもとても有効です。
生徒は他の生徒の解法をみることで、より良い解法に気づくことができます。


参考リンク
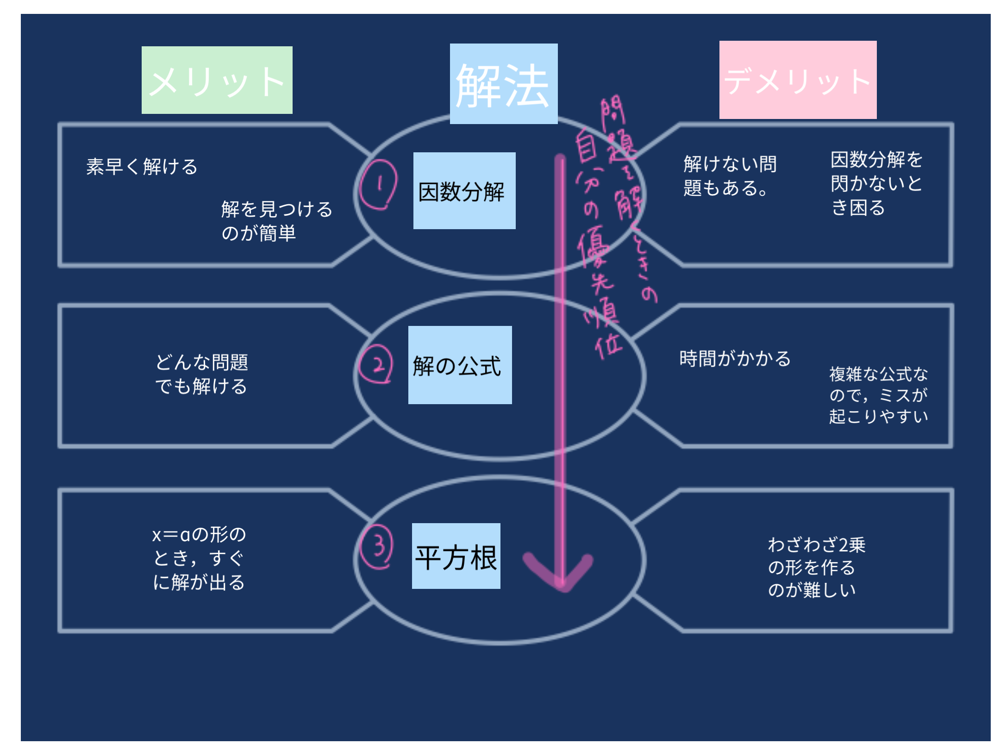
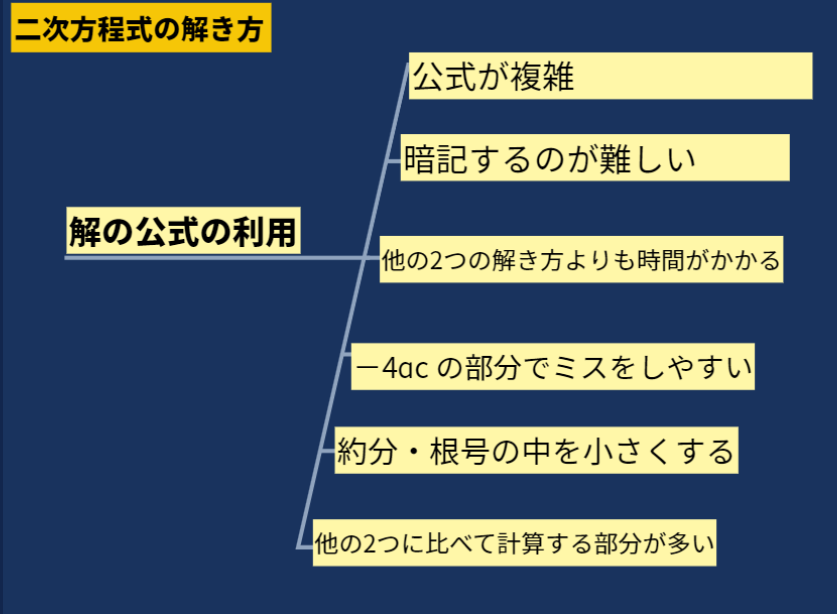
シンキングツールで解法を整理
1つの問題に対して複数の立式や解法が存在するこの分野では、解放の特徴をシンキングツールで整理することがとても有効です。
生徒は解放ごとの特徴をシンキングツールで整理することでより効果的なアプローチを模索しやすくなります。

参考リンク
共有ノートでリアルタイムに意見を共有しながら解き進める
習熟度に差がでやすいこの分野では、共有ノートでお互いの考えをリアルタイムで共有しながら学びを進めるアプローチがとても有効です。
生徒は問題を解く課程から意見を交換することで、難しい問題にもチャレンジしやすくなります。
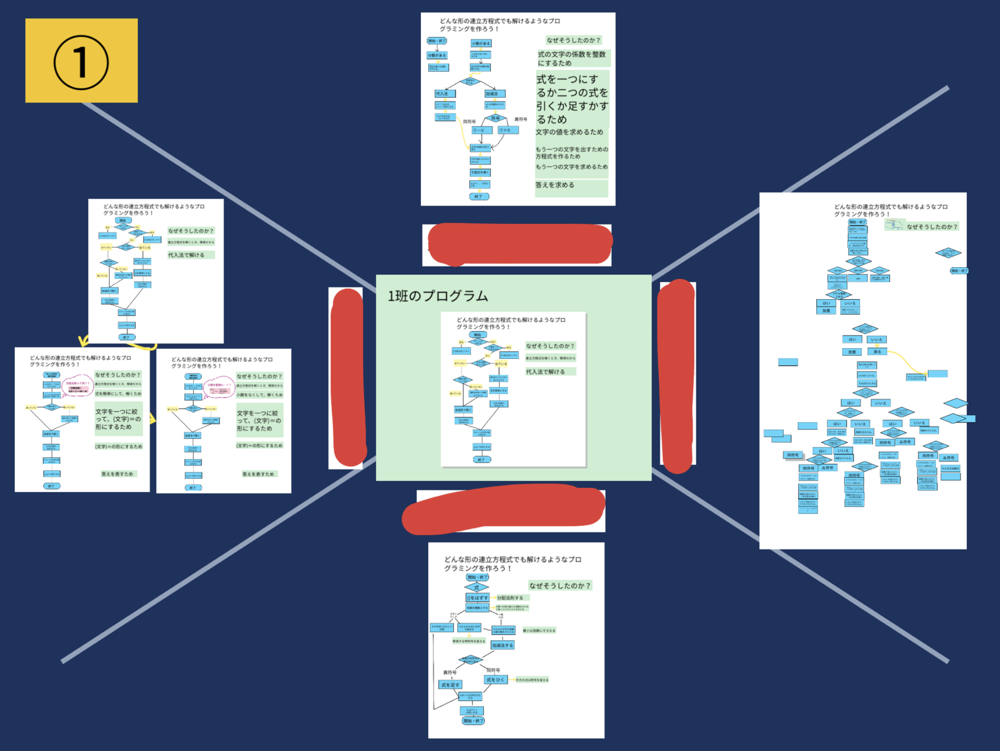
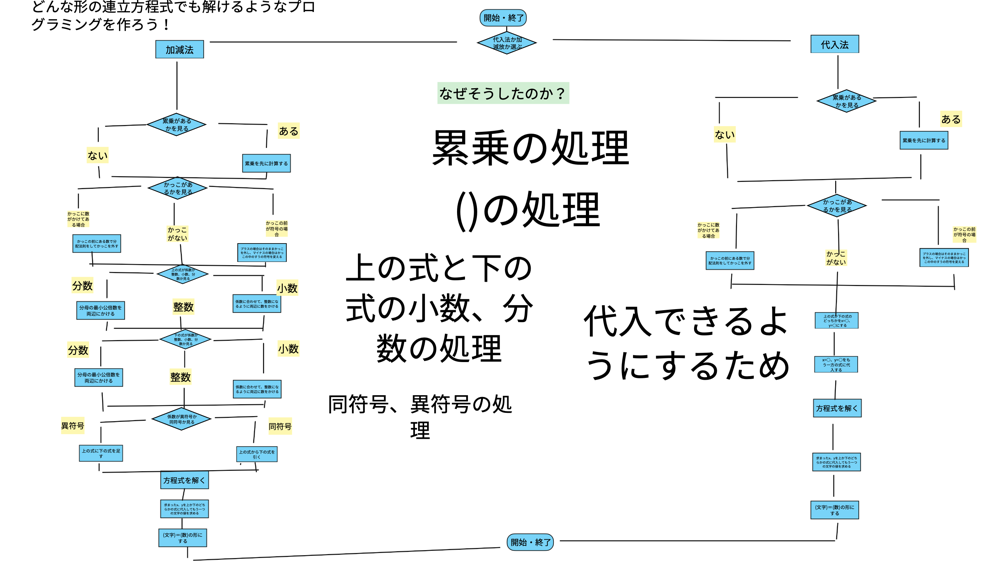

参考リンク
図形に関する内容
平面図形と空間図形
作図、図形の移動、三角形や多角形の性質、図形の合同・相似、円周角・三平方の定理などを通して、図形の特徴と証明の考え方を身にけるこの分野では、手書きで補助線などを書き込むことで理解がしやすくなります。
また、シンキングツールでそれぞれの図形や定理の特徴をまとめることで理解を深めることができます。
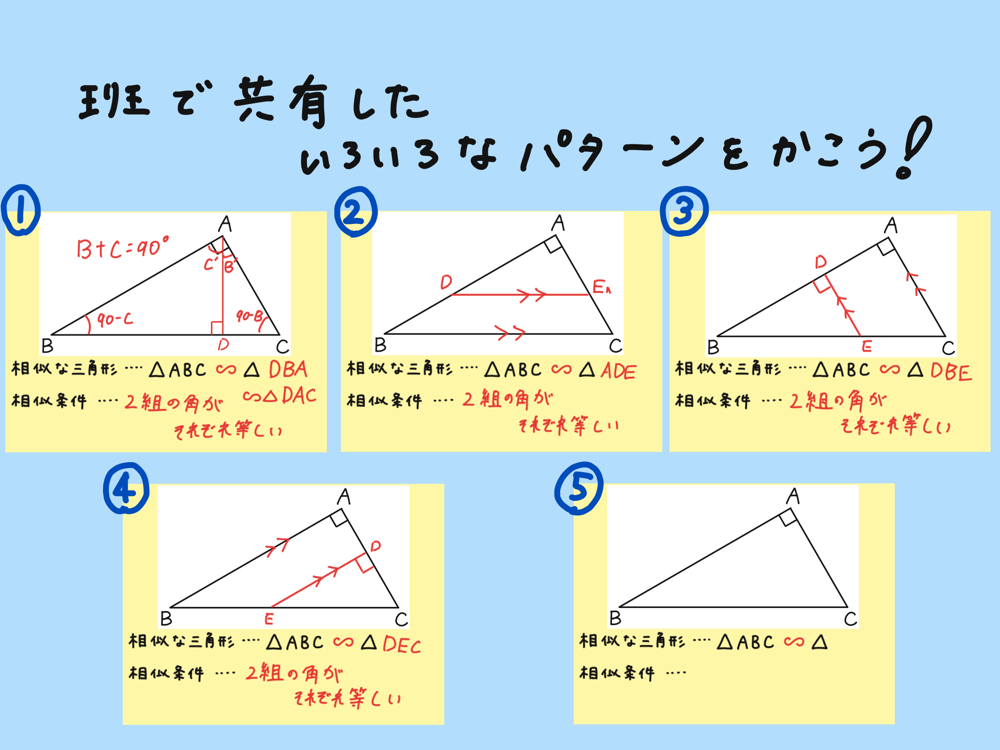
手書き・定規ツールで理解を深める
ロイロでは紙に書いているような滑らかな感覚で簡単に手書きを加えることができます。また、定規ツールで任意の角度の直線を引くことも可能です。
手書き・定規ツールで自由に書き込むことで解法が理解しやすくなります。
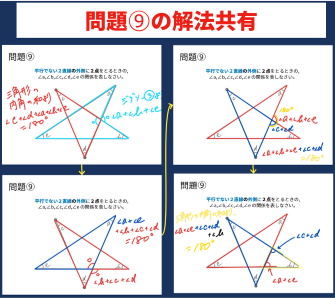
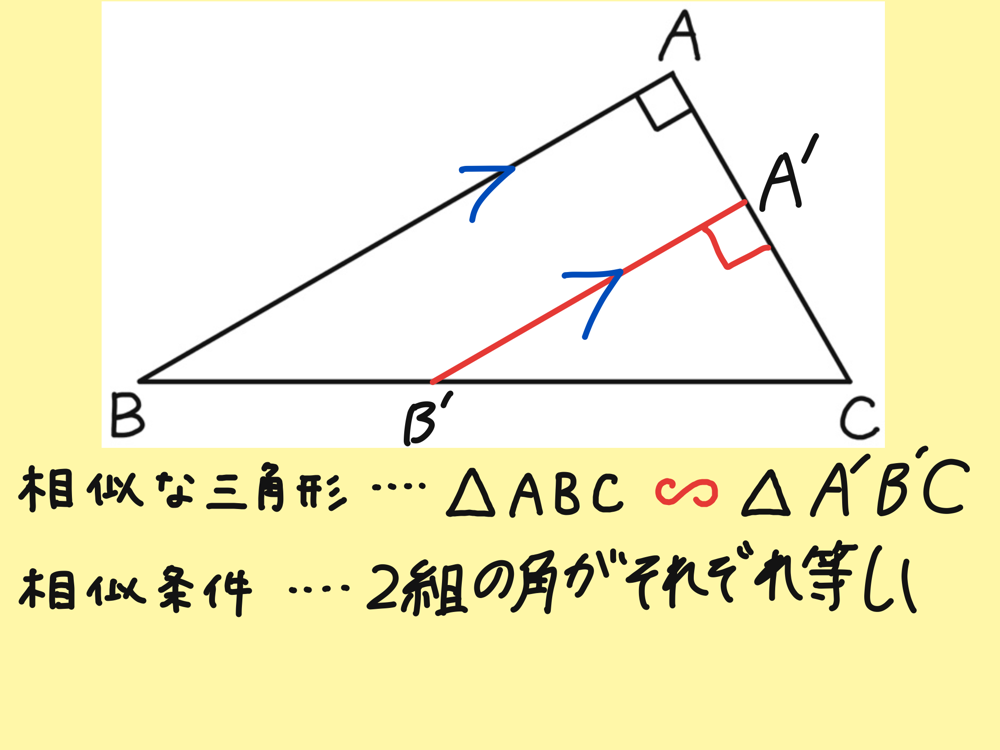
参考リンク
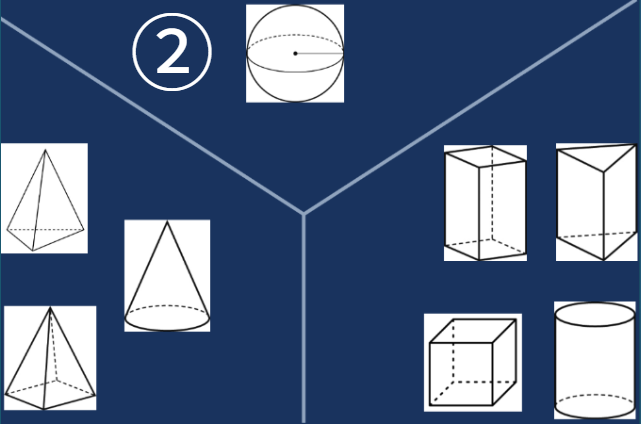
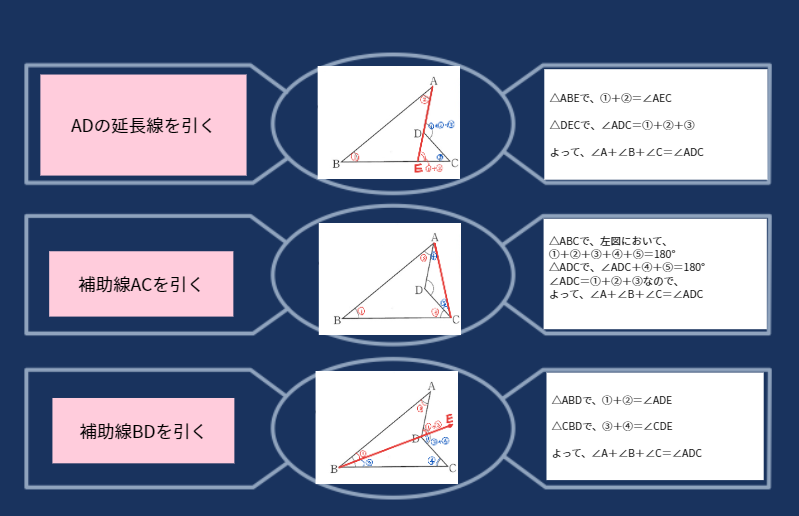
シンキングツールで図形や定理の特徴、解法を整理する
シンキングツールをつかって、同じ視点から、図形・定理の性質をまとめることで理解がしやすくなります。
また解法をキングツールで整理することで、新たな視点で問題を解くことができるようになります。

参考リンク
座標と方程式
座標の意味や直線・円の方程式、点と直線の距離、図形の性質の証明、軌跡や領域の考察などを通して、図形と代数のつながりを学ぶこの分野では、公式の使い分けが難しく、シンキングツールによって特徴を整理することがとても有効になります。
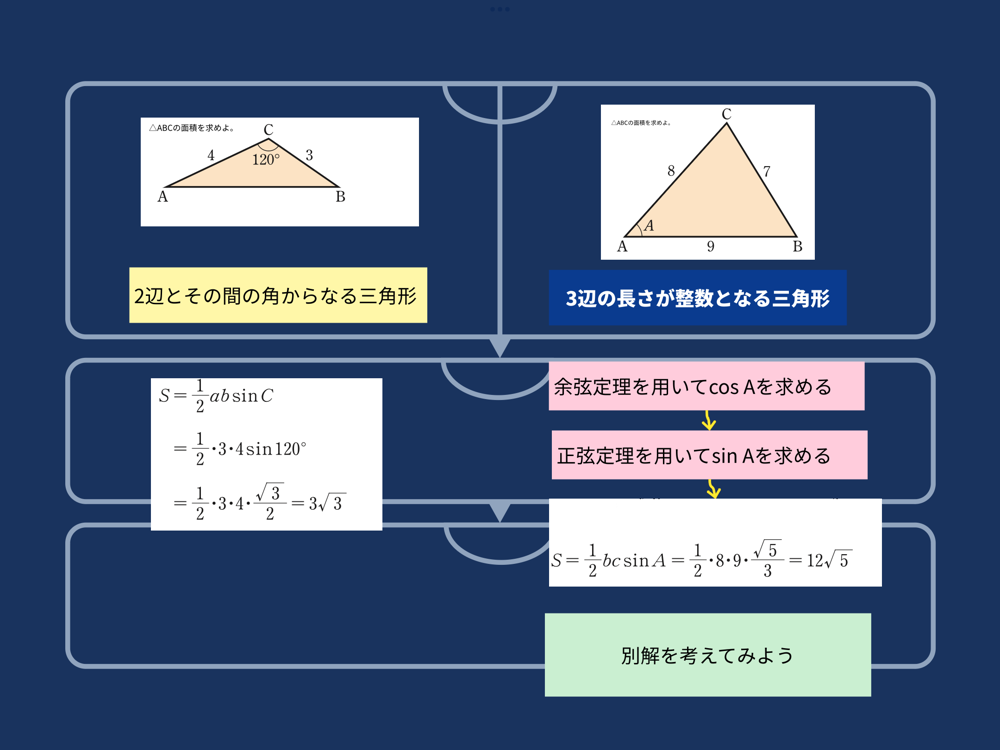
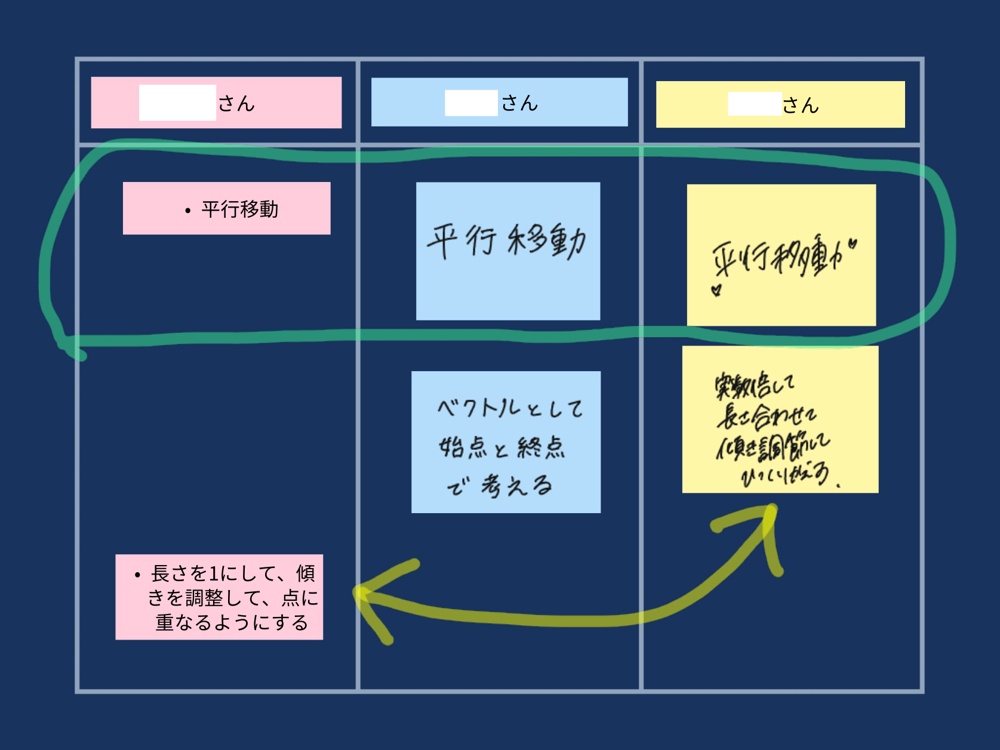
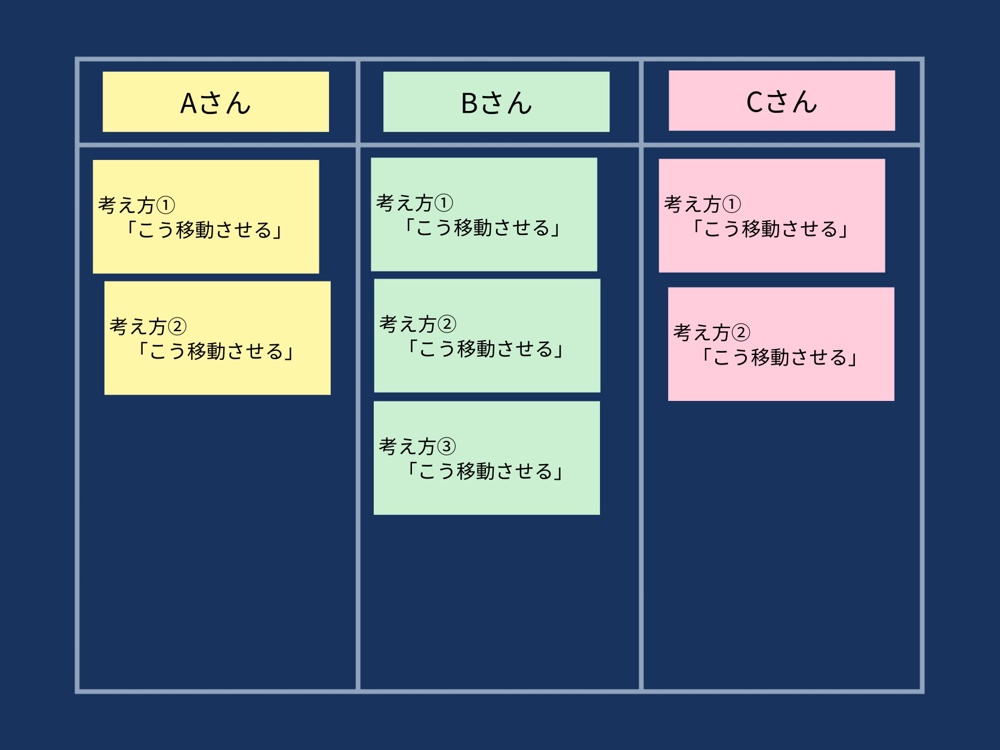
シンキングツールを使って公式の特徴をまとめる
シンキングツールを使うことによって、使い分けが難しいこの分野の公式も理解しやすくなります。
さらに、共有ノート上でシンキングツールを活用することによって、より多角的な視点から解法を整理することもできます。
参考リンク
関数に関する内容
各種関数について
比例・反比例・一次関数・二次関数などの基本的な関数から、三角関数・指数関数・対数関数まで、さまざまな関数の特徴と使い方を理解するこの単元では、webカードをつかって、GeoGebraなどのグラフを自由に作成する機能を使うことがとても便利です。
また、シンキングツールを活用することによって、グラフの条件検討などがしやすくなります。
webカード(GeoGebra)をつかって自由にグラフを動かして考える
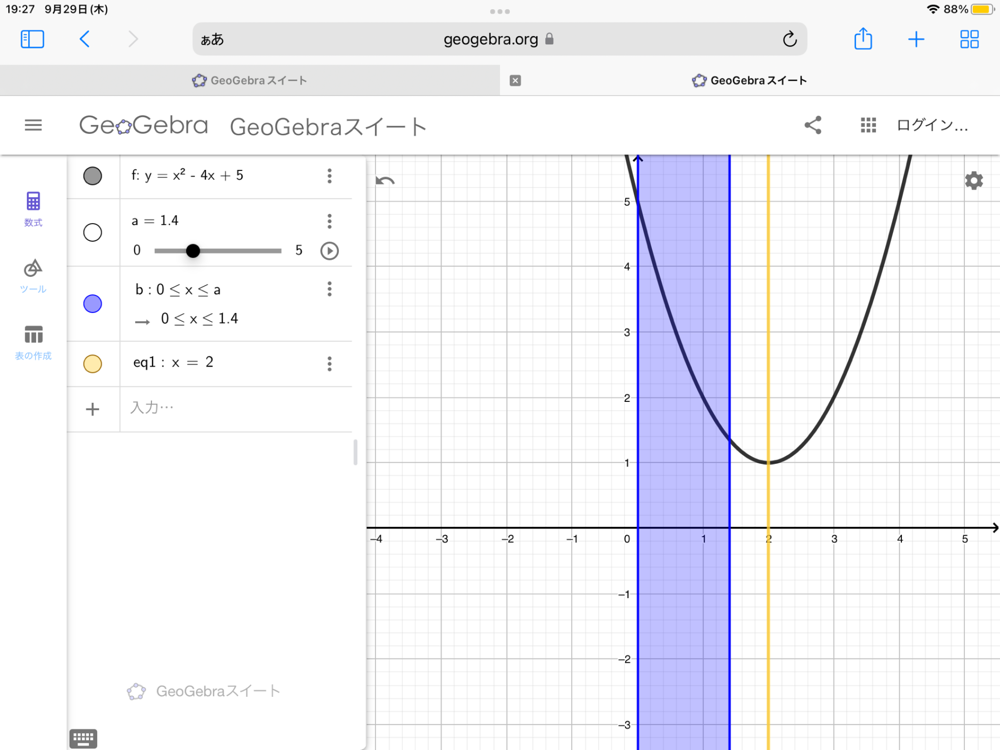
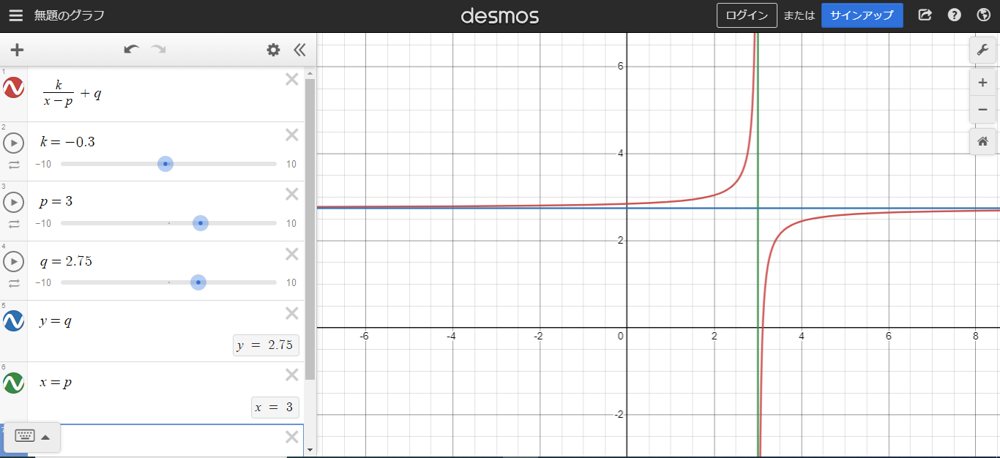
頂点や軸の変化をとらえることが重要となるこの分野では、webカードをつかってGeoGebraなどのグラフを作成できるページを共有するのが非常に便利です。
生徒は自由にグラフを移動・変形させることで、関数とグラフの性質を理解しやすくなります。

参考リンク
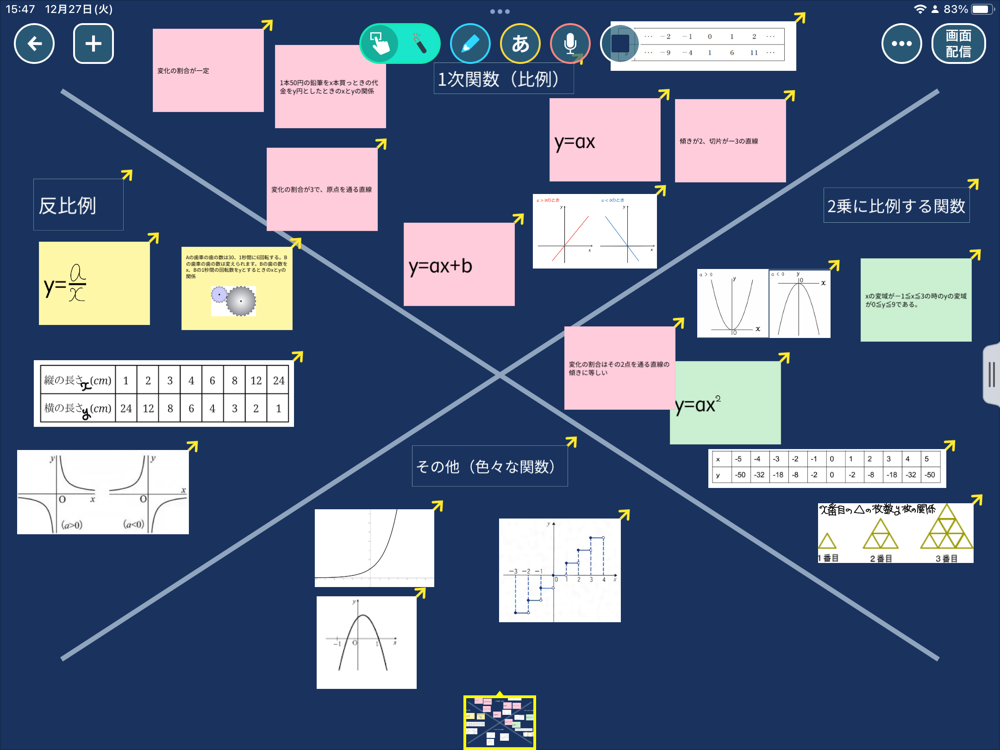
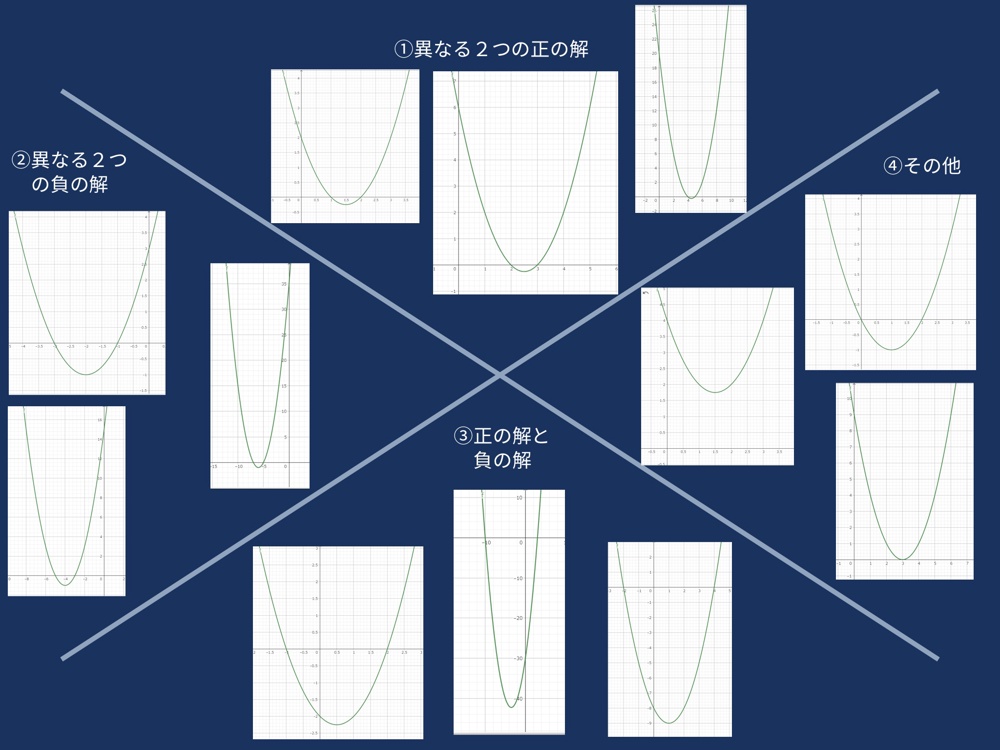
シンキングツールでグラフの特徴や条件を整理
関数の分野では、頂点や軸、変曲点の変化などを捉えることがとても大切になってきます。シンキングツールをつかってそういった関数に関する特徴や条件を整理することによって理解をふかめやすくなります。

参考リンク
データの活用と確率に関する内容
データの収集と分析
データを集め、表やグラフに整理し、四分位数や標準偏差、散布図や相関係数などを用いて、データの傾向や関係を分析する力を養う分野では、アンケートカードをつかって、分析に用いるデータを簡単にあつめることができます。
また、シンキングツールをつかって分析結果をまとめることで、読み取りがしやすくなります。
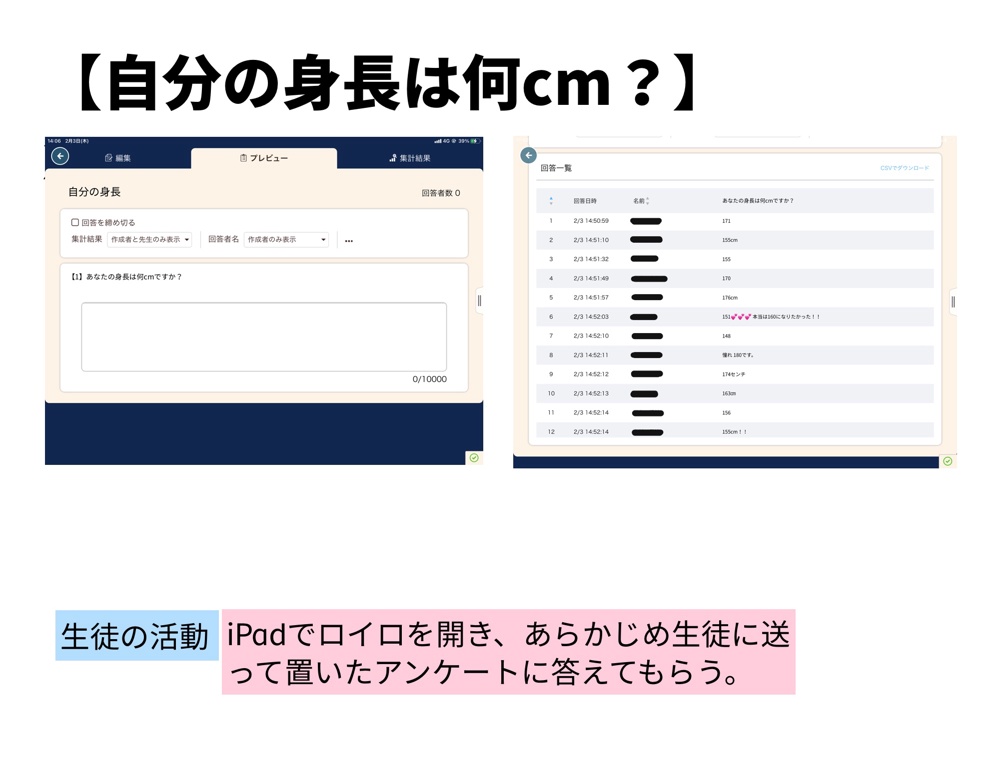
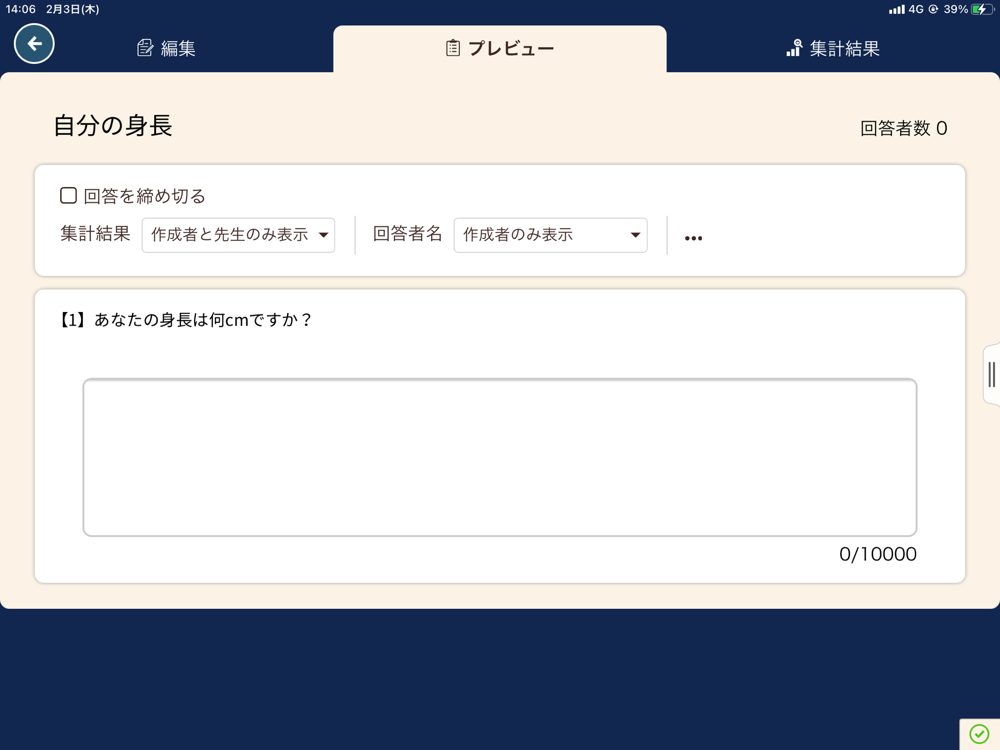
アンケートカードでデータの収集
データの収集と分析の分野では、分析する材料となるデータを集める必要があります。
ロイロのアンケートカードは、生徒が作成することができ、生徒同士でアンケートをとることもできるため、データの収集を簡単におこなうことができます。
参考リンク
シンキングツールで分析したデータを考察
シンキングツールでデータから読み取った内容をまとめることで、データの分析もスムーズになります。
視点を設定してデータや読み取れた内容をまとめていくことで、生徒はデータから読み取った内容を深く考えることができるようになります。
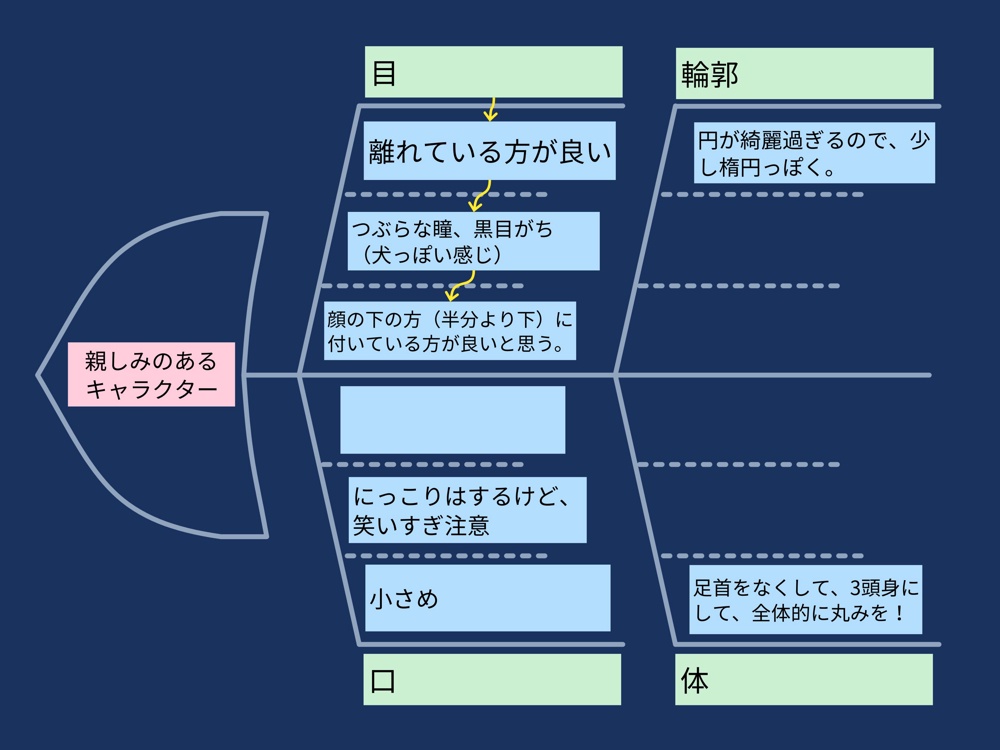
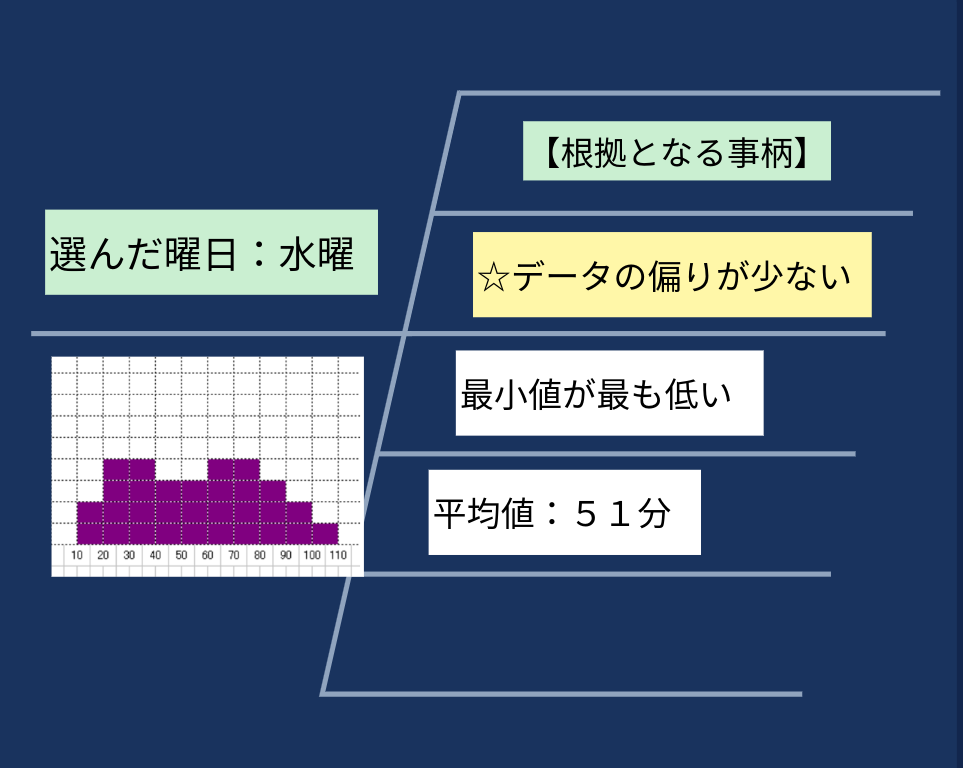
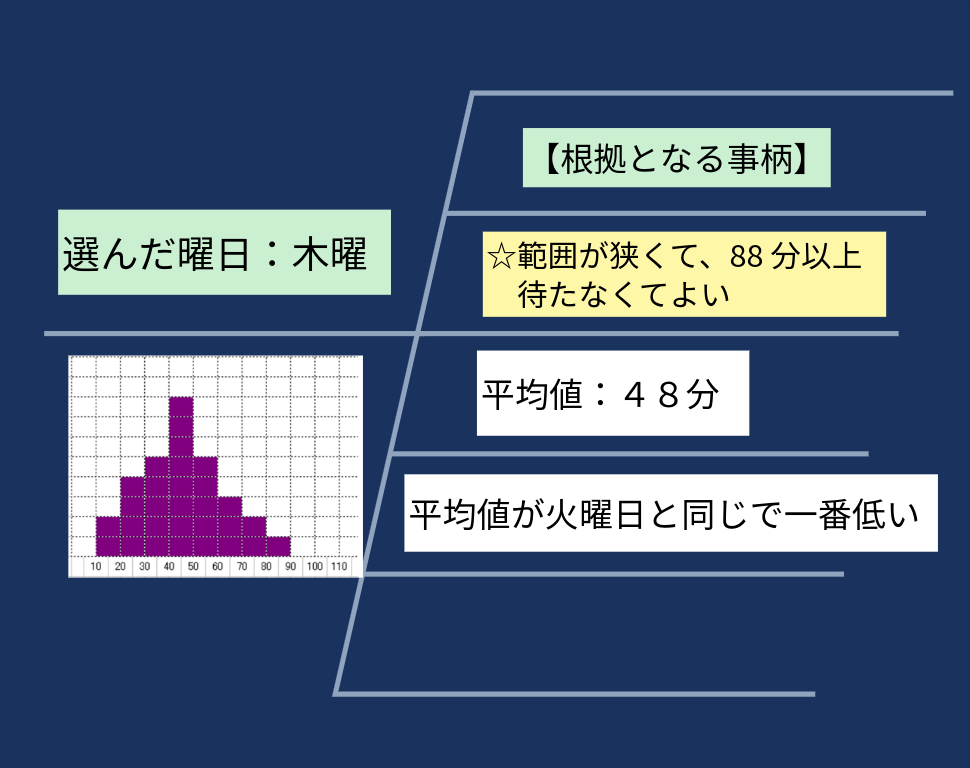
参考リンク
確率と場合の数
場合の数を基にした確率の考え方や、多数回の試行から確率の意味を理解し、身近な事象の分析に生かす分野では、カードを並べ替えたり動かすことができるロイロの機能がとても便利です。
カードをうごかして場合の数を数え上げ
ロイロでは、カードの中にはいったカードを簡単に動かすことができます。またカードの複製も簡単です。そのため、場合の数を学ぶ際に、実際に組み合わせを考えて数え上げることができます。


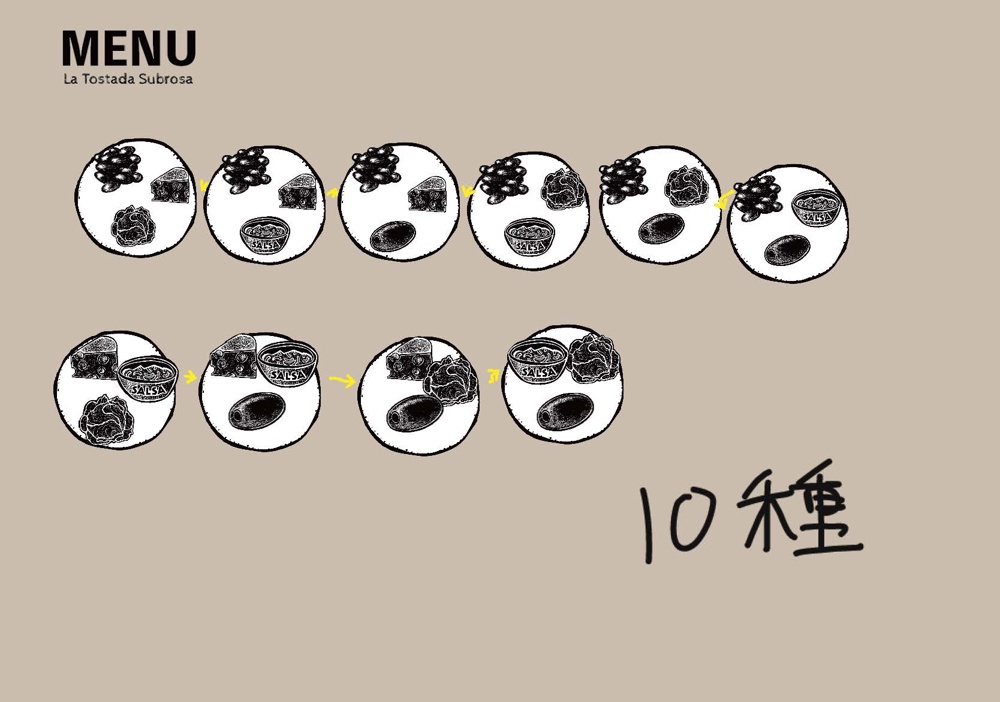
参考リンク
認定ティーチャーによる数学でのロイロ活用法まとめ
ロイロ認定ティーチャーによる中学校・高校での数学の活用事例をまとめました
認定ティーチャーの授業案を検索する
以下のページから全国のロイロ認定ティーチャーの授業案を検索することができます。
授業案で使われているワークシートはそのまま、ご自身のロイロに取り込んで活用することができます。授業実践にご利用ください。
教科別活用法にもどる